On Relative Growings

All through the calculus we are dealing with quantities that are growing, and with rates of growth. We classify all quantities into two classes: constants and variables. Those which we regard as of fixed value, and call constants, we generally denote algebraically by letters from the beginning of the alphabet, such as $a$, $b$, or $c$; while those which we consider as capable of growing, or (as mathematicians say) of “varying,” we denote by letters from the end of the alphabet, such as $x$, $y$, $z$, $u$, $v$, $w$, or sometimes $t$.

Moreover, we are usually dealing with more than one variable at once, and thinking of the way in which one variable depends on the other: for instance, we think of the way in which the height reached by a projectile depends on the time of attaining that height. Or we are asked to consider a rectangle of given area, and to enquire how any increase in the length of it will compel a corresponding decrease in the breadth of it. Or we think of the way in which any variation in the slope of a ladder will cause the height that it reaches, to vary.

Suppose we have got two such variables that depend one on the other. An alteration in one will bring about an alteration in the other, because of this dependence. Let us call one of the variables $x$, and the other that depends on it $y$.

Suppose we make $x$ to vary, that is to say, we either alter it or imagine it to be altered, by adding to it a bit which we call $dx$. We are thus causing $x$ to become $x + dx$. Then, because $x$ has been altered, $y$ will have altered also, and will have become $y + dy$. Here the bit $dy$ may be in some cases positive, in others negative; and it won't (except by a miracle) be the same size as $dx$.

Take two examples.

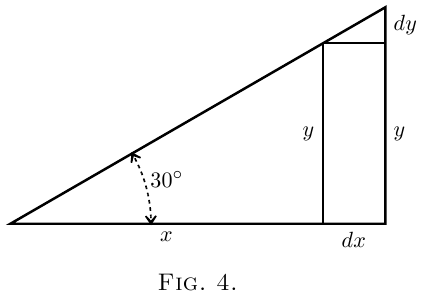
(1) Let $x$ and $y$ be respectively the base and the height of a right-angled triangle (Figure 4), of which the slope of the other side is fixed at $30°$. If we suppose this triangle to expand and yet keep its angles the same as at first, then, when the base grows so as to become $x + dx$, the height becomes $y + dy$. Here, increasing $x$ results in an increase of $y$. The little triangle, the height of which is $dy$, and the base of which is $dx$, is similar to the original triangle; and it is obvious that the value of the ratio $\dfrac{dy}{dx}$ is the same as that of the ratio $\dfrac{y}{x}$. As the angle is $30°$ it will be seen that here \[ \frac{dy}{dx} = \frac{1}{1.73}. \]

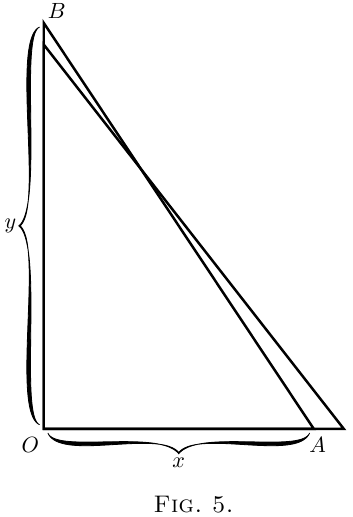
(2) Let $x$ represent, in Figure 5, the horizontal distance, from a wall, of the bottom end of a ladder, $AB$, of fixed length; and let $y$ be the height it reaches up the wall. Now $y$ clearly depends on $x$. It is easy to see that, if we pull the bottom end $A$ a bit further from the wall, the top end $B$ will come down a little lower. Let us state this in scientific language. If we increase $x$ to $x + dx$, then $y$ will become $y - dy$; that is, when $x$ receives a positive increment, the increment which results to $y$ is negative.

Yes, but how much? Suppose the ladder was so long that when the bottom end $A$ was $19$ inches from the wall the top end $B$ reached just $15$ feet from the ground. Now, if you were to pull the bottom end out $1$ inch more, how much would the top end come down? Put it all into inches: $x = 19$ inches, $y = 180$ inches. Now the increment of $x$ which we call $dx$, is $1$ inch: or $x + dx = 20$ inches.

How much will $y$ be diminished? The new height will be $y - dy$. If we work out the height by Euclid I. 47, then we shall be able to find how much $dy$ will be. The length of the ladder is \[ \sqrt{ (180)^2 + (19)^2 } = 181 \text{ inches}. \] Clearly then, the new height, which is $y - dy$, will be such that \begin{align*} (y - dy)^2 &= (181)^2 - (20)^2 = 32761 - 400 = 32361, \\ y - dy &= \sqrt{32361} = 179.89 \text{ inches}. \end{align*} Now $y$ is $180$, so that $dy$ is $180 - 179.89 = 0.11$ inch.

So we see that making $dx$ an increase of $1$ inch has resulted in making $dy$ a decrease of $0.11$ inch.

And the ratio of $dy$ to $dx$ may be stated thus: \[ \frac{dy}{dx} = - \frac{0.11}{1}. \]

It is also easy to see that (except in one particular position) $dy$ will be of a different size from $dx$.

Now right through the differential calculus we are hunting, hunting, hunting for a curious thing, a mere ratio, namely, the proportion which $dy$ bears to $dx$ when both of them are indefinitely small.

It should be noted here that we can only find this ratio $\dfrac{dy}{dx}$ when $y$ and $x$ are related to each other in some way, so that whenever $x$ varies $y$ does vary also. For instance, in the first example just taken, if the base $x$ of the triangle be made longer, the height $y$ of the triangle becomes greater also, and in the second example, if the distance $x$ of the foot of the ladder from the wall be made to increase, the height $y$ reached by the ladder decreases in a corresponding manner, slowly at first, but more and more rapidly as $x$ becomes greater. In these cases the relation between $x$ and $y$ is perfectly definite, it can be expressed mathematically, being $\dfrac{y}{x} = \tan 30°$ and $x^2 + y^2 = l^2$ (where $l$ is the length of the ladder) respectively, and $\dfrac{dy}{dx}$ has the meaning we found in each case.

If, while $x$ is, as before, the distance of the foot of the ladder from the wall, $y$ is, instead of the height reached, the horizontal length of the wall, or the number of bricks in it, or the number of years since it was built, any change in $x$ would naturally cause no change whatever in $y$; in this case $\dfrac{dy}{dx}$ has no meaning whatever, and it is not possible to find an expression for it. Whenever we use differentials $dx$, $dy$, $dz$, etc., the existence of some kind of relation between $x$, $y$, $z$, etc., is implied, and this relation is called a “function” in $x$, $y$, $z$, etc.; the two expressions given above, for instance, namely $\dfrac{y}{x} = \tan 30°$ and $x^2 + y^2 = l^2$, are functions of $x$ and $y$. Such expressions contain implicitly (that is, contain without distinctly showing it) the means of expressing either $x$ in terms of $y$ or $y$ in terms of $x$, and for this reason they are called implicit functions in $x$ and $y$; they can be respectively put into the forms \begin{align*} y &= x \tan 30° \quad\text{or}\quad x = \frac{y}{\tan 30°} \\ \text{and}\; y &= \sqrt{ l^2 - x^2} \quad\text{or}\quad x = \sqrt{ l^2 - y^2}. \end{align*}

These last expressions state explicitly (that is, distinctly) the value of $x$ in terms of $y$, or of $y$ in terms of $x$, and they are for this reason called explicit functions of $x$ or $y$. For example $x^2 + 3 = 2y - 7$ is an implicit function in $x$ and $y$; it may be written $y = \dfrac{x^2 + 10}{2}$ (explicit function of $x$) or $x = \sqrt{2y - 10}$ (explicit function of $y$). We see that an explicit function in $x$, $y$, $z$, etc., is simply something the value of which changes when $x$, $y$, $z$, etc., are changing, either one at the time or several together. Because of this, the value of the explicit function is called the dependent variable, as it depends on the value of the other variable quantities in the function; these other variables are called the independent variables because their value is not determined from the value assumed by the function. For example, if $u = x^2 \sin \theta$, $x$ and $\theta$ are the independent variables, and $u$ is the dependent variable.

Sometimes the exact relation between several quantities $x$, $y$, $z$ either is not known or it is not convenient to state it; it is only known, or convenient to state, that there is some sort of relation between these variables, so that one cannot alter either $x$ or $y$ or $z$ singly without affecting the other quantities; the existence of a function in $x$, $y$, $z$ is then indicated by the notation $F(x, y, z)$ (implicit function) or by $x = F(y, z)$, $y = F(x, z)$ or $z = F(x, y)$ (explicit function). Sometimes the letter $f$ or $\phi$ is used instead of $F$, so that $y = F(x)$, $y = f(x)$ and $y = \phi(x)$ all mean the same thing, namely, that the value of $y$ depends on the value of $x$ in some way which is not stated.

We call the ratio $\dfrac{dy}{dx}$ “the differential coefficient of $y$ with respect to $x$.” It is a solemn scientific name for this very simple thing. But we are not going to be frightened by solemn names, when the things themselves are so easy. Instead of being frightened we will simply pronounce a brief curse on the stupidity of giving long crack-jaw names; and, having relieved our minds, will go on to the simple thing itself, namely the ratio $\dfrac{dy}{dx}$.

In ordinary algebra which you learned at school, you were always hunting after some unknown quantity which you called $x$ or $y$; or sometimes there were two unknown quantities to be hunted for simultaneously. You have now to learn to go hunting in a new way; the fox being now neither $x$ nor $y$. Instead of this you have to hunt for this curious cub called $\dfrac{dy}{dx}$. The process of finding the value of $\dfrac{dy}{dx}$ is called “differentiating.” But, remember, what is wanted is the value of this ratio when both $dy$ and $dx$ are themselves indefinitely small. The true value of the differential coefficient is that to which it approximates in the limiting case when each of them is considered as infinitesimally minute.

Let us now learn how to go in quest of $\dfrac{dy}{dx}$.

NOTE TO CHAPTER III.

Another way of indicating that a function has been differentiated is by putting an accent to the symbol of the function. Thus if $y=F(x)$, which means that $y$ is some unspecified function of $x$ (see here), we may write $F'(x)$ instead of $\dfrac{d\bigl(F(x)\bigr)}{dx}$. Similarly, $F''(x)$ will mean that the original function $F(x)$ has been differentiated twice over with respect to $x$.